There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Example 1:
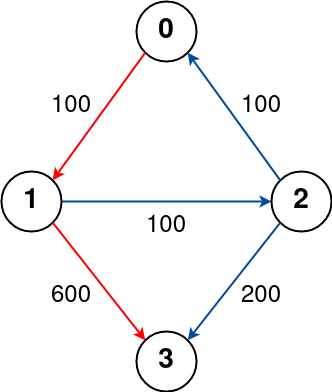
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1 Output: 700 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700. Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.
Example 2:
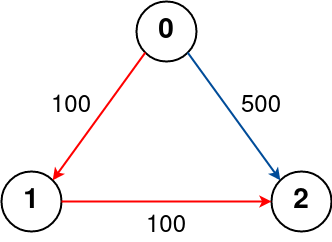
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 Output: 200 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
Example 3:
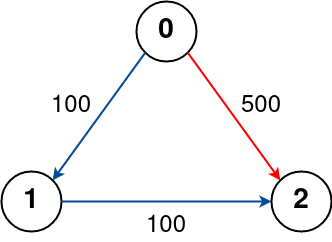
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0 Output: 500 Explanation: The graph is shown above. The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
Constraints:
1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= fromi, toi < nfromi != toi1 <= pricei <= 104- There will not be any multiple flights between two cities.
0 <= src, dst, k < nsrc != dst
This problem can be solved via Dijkstra’s algorithm as well. The tricky part is there are two factors. One is price, the other one is how many stops. Price is the first priority when the stops is less than k.
Therefore, when stop is greater than k, then it’s no need to keep looking.
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
graph = {}
for i in range(n):
graph[i] = []
for flight in flights:
graph[flight[0]].append((flight[2], flight[1]))
shortest = [101 for i in range(n)]
minHeap = [(0, src, -1)]
while minHeap:
price, dest, stop = heapq.heappop(minHeap)
if stop > k or stop > shortest[dest]:
continue
if dest == dst:
return price
shortest[dest] = stop
connected_flights = graph[dest]
for flight in connected_flights:
heapq.heappush(minHeap, (price+flight[0], flight[1], stop+1))
return -1

搶先發佈留言