Leetcode 79. Word Search

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example 1:

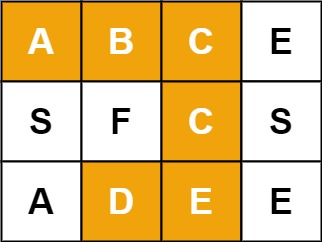
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true

Example 2:

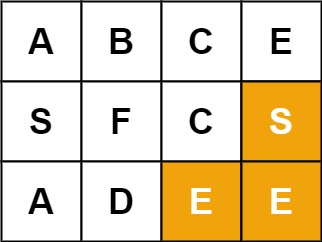
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true

Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false

Constraints:

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board and word consists of only lowercase and uppercase English letters.

Follow up: Could you use search pruning to make your solution faster with a larger board?

This is my first daily problem and not hard to figure it out that it can be solved by DFS.

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]

        m = len(board)
        n = len(board[0])

        for i in range(m):
            for j in range(n):
                if board[i][j] == word[0]:
                    if self.find_word(board, word, i, j, 1):
                        return True

        return False

    def find_word(self, board, word, i, j, same_len):
        if len(word) == same_len:
            return True

        directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]

        m = len(board)
        n = len(board[0])

        current = board[i][j]
        board[i][j] = None

        for direction in directions:
            new_i = i + direction[0]
            new_j = j + direction[1]

            if 0 <= new_i < m and 0 <= new_j < n and board[new_i][new_j] is not None:
                if board[new_i][new_j] == word[same_len]:
                    result = self.find_word(board, word, new_i, new_j, same_len + 1)

                    if result:
                        return True
        
        board[i][j] = current
        
        return False